krachten die werken op een constructie

ik heb een paar vragen waar hopelijk snel antwoord op kan worden gegeven:
1- heeft een materiaalkeuze iets te maken met het aantal krachten die dan op een constructie werken?
2- wat is de sterkste en wat is de zwakste constructie?
3- Hoe kan je die krachten ontbinden of samenstellen?
4- Wat zijn duwkrachten en wat zijn trekkrachten bij een constructie?
5- Hoe groot kan zo’n kracht worden?

Het zijn nogal wat vragen. En er zijn nogal wat constucties mogelijk, van een simpel huis tot een brug of een draaiende kermisattractie. Al deze constructies hebben echter ??n ding gemeen: ze hebben van nature de neiging om naar beneden te willen richting aarde.

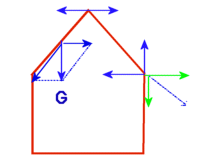Laten we aan de hand van een simpele tekening van een kerkje es kijken wat er voor krachten optreden als gevolg van het dak. Het dak heeft een bepaald gewicht [G]. Ik heb dit hier alleen voor de linker helft van het dak getekend, maar uiteraard heeft de rechter helft dit ook.

Deze kracht kun je ontbinden in 2 andere krachten. E?n die evenwijdig loopt aan het dak (een kracht loopt altijd langs een lijn) en ??n die horizontaal loopt. Je moet je dit een beetje als volgt voor kunnen stellen: De linker kant van het dak wil naar rechts kantelen. Er is aan de bovenkant dus een kracht naar rechts. Als het dak mooi symetrisch is wil de rechter kant van het dak met een evengrote kracht naar links, zodat er evenwicht is.

Dan de onderkant van het dak: De kracht evenwijdig aan het dak kun je ontbinden in 2 vectoren. De kracht zelf mag je langs een lijn verplaatsen. Dit is rechts getekend. Deze kracht op de muur is ontbonden in een horizontale en een verticale component (de 2 groene vectoren) De verticale kracht is het gewicht van het dak wat op de muur drukt en de horizontale kracht wil de muur wegdrukken. Dit kun je visualiseren door dit als een papier kerkje te zien: Als je op de aangrijpingspunten van de zwaartekracht [G] van het dak drukt willen de zij kanten naar buiten. Op het dak zelf werken de evengrote maar tegenovergestelde krachten. Stel dat je de onderkant van het dak met de hand op zijn plaats moet houden, dan zou je het omhoog en naar binnen moeten drukken. De kracht die jij op dat moment op het dak uit moet oefenen moet even groot zijn als als de ontbonden vectoren. Druk je met een te kleinere kracht omhoog, dan is er geen krachtevenwicht en gaat het dak naar beneden. Vang je wel het gewicht op, maar druk je onvoldoende naar binnen, dan gaat het dak naar buiten. Op een constructie die in evenwicht is, dus die niet beweegt, zijn de krachten altijd in evenwicht.

Bij een gewoon huis zet men nu een dwarsbalk vast op de onderkanten van de dakdelen. Op deze dwarsbalk komt dan de trekkracht te staan en de muren hoeven alleen het gewicht (drukkracht) op te vangen. Bij een (ouderwetse) kerk vond men de dwarsbalken ontsierend. Om de (druk) krachten die dan op de muur werken op te vangen werden er aan de buitenkant van de kerk z.g. steunberen gemetseld. Deze zorgen er dan voor dat de muur niet naar buiten word gedrukt.

Om op de vragen terug te komen: De materiaal keuze heeft geen invloed op het aantal krachten, maar wel op de grootte van de krachten. Als het materiaal op druk wordt belast (gewicht dak), zoals de muren is er sprake van drukkrachten. In het getekende voorbeeld wordt de muur dus ook nog op dwarsdruk belast. Zou je een dwarsbalk aanbrengen, dan valt de dwarsdrukkracht op de muur weg, en staat er op de dwarsbalk een trekkracht. Krachten kunnen zo groot worden dat de constuctie het begeeft. Als ik besluit om loden dakpannen op det dak te leggen en er bovendien nog wat grote zware gietijzeren kroonluchters aan hang neemt de kracht [G] enorm toe. De pijl wordt dus langer en ook alle ontbonden krachten.

**arjen**